Hệ thức Viet được sử dụng trong nhiều dạng toán và bài tập thuộc phần kiến thức về phương trình bậc hai một ẩn. Đây cũng là nội dung thường xuất hiện trong đề thi tuyển sinh vào lớp 10 THPT. Vậy hệ thức Viet x1-x2 áp dụng cho dạng bài toán nào? Hãy cùng đăng nhập kubet77 tìm hiểu qua bài viết này. Đồng thời vận dụng các công thức tiếng việt để giải một số bài toán có liên quan nhằm rèn luyện năng lực học toán cho trẻ.
Định lý Viet
Định lý Viet hay hệ thức Viet x1-x2 biểu thị mối quan hệ giữa các nghiệm của phương trình đa thức do nhà toán học người Pháp François Viète tìm ra.
Hệ thức Viet x1-x2
Cho phương trình bậc 2 một ẩn: ax2+bx+c=0 (a≠0) (*) có 2 nghiệm x1 và x2. Khi đó 2 nghiệm này thỏa mãn hệ thức sau:
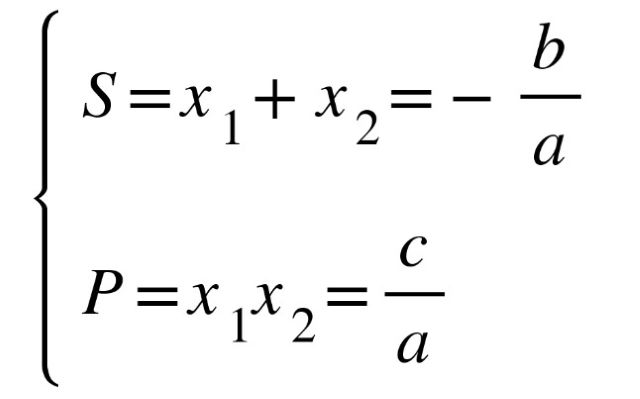
Hệ quả: Theo hệ thức Viet x1-x2 khi phương trình bậc hai có nghiệm ta có thể tính trực tiếp nghiệm của phương trình trong một số trường hợp đặc biệt:
- Nếu a+b+c=0 thì (*) có 1 nghiệm x1=1 và x2=c/a
- Nếu a-b+c=0 thì (*) có nghiệm x1=-1 và x2=-c/a
>>> Có thể bạn quan tâm: Lên giải trong liên quân là gì? Cách Lên giải cho SP 2023
Định lý Viet mở rộng
Nội dung hệ thức Viet mở rộng như sau: Giả sử hai số thực x1 và x2 thỏa mãn hệ thức:
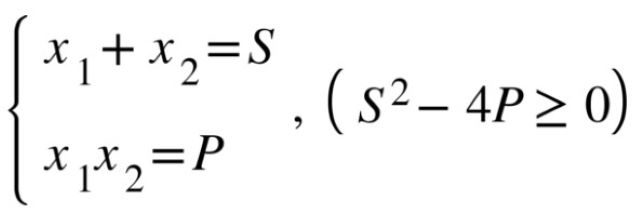
thì x1 và x2 là 2 nghiệm của phương trình bậc 2: x2-Sx+P=0 (1).
Chú ý: điều kiện S2-4P≥0 là bắt buộc. Đây là điều kiện để ∆(1)≥0 hay nói cách khác, đây là điều kiện để phương trình bậc 2 tồn tại nghiệm.
Ứng dụng hệ thức viet x1-x2
Là kiến thức trọng tâm của khối THCS, dạng bài áp dụng hệ thức Viet x1-x2 vô cùng đa dạng. Sau đây bài viết sẽ hướng dẫn các em các dạng toán cụ thể áp dụng hệ thức viet bậc 2.
Dạng 1: Biểu thức liên hệ giữa 2 nghiệm
Khi làm dạng bài tập này, học sinh cần nhận biết được sự tồn tại nghiệm của phương trình, từ đó phát biểu các biểu thức dưới dạng x1+x2 và x1.x2 để vận dụng định lý Vi-et. Các hằng đẳng thức thường dùng là:
a2 + b2 = (a+b)2 – 2ab
a3 + b3 = (a+b)3 – 3ab(a+b)
Dạng 2: Hệ đối xứng hai ẩn kiểu 1 là hệ gồm hai phương trình hai ẩn.
Trong đó mỗi phương trình giữ nguyên nếu chúng ta hoán đổi vai trò của các ẩn số trong mỗi phương trình. Để giải hệ đối xứng loại 1 bằng hệ thức Viet x1-x2, thông thường ta biểu diễn phương trình dưới dạng tổng và tích hai ẩn số. Các hằng đẳng thức được sử dụng phổ biến nhất là:
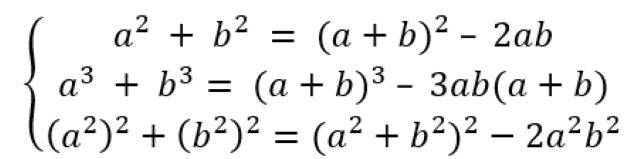
Dạng 3: Chứng minh bất đẳng thức
Hệ thức Viet x1-x2 vẫn có thể được dùng để chứng minh các bất đẳng thức. Tất nhiên, ở đây chúng tôi đề cập đến việc sử dụng nó để chuyển đổi trung gian. Để có thể sử dụng định lý Viet, dữ liệu của bài toán thường được trả về dưới dạng tổng và tích các ẩn số. Quá trình chứng minh có thể sử dụng định lý dấu của tam thức bậc hai, các bất phương trình cổ điển, các phép biến đổi tương đương.
Dạng 4: Ứng dụng vào bài toán tính cực trị của hàm số
Đây là dạng câu hỏi tương đối phổ biến trong các đề thi đại học những năm gần đây, trọng tâm của dạng câu hỏi này là làm thế nào để học sinh có thể diễn đạt tọa độ cực một cách ngắn gọn và nhanh chóng nhất.
Dạng 5: Ứng dụng vào bài toán tiếp tuyến
Các bài tập về tiếp tuyến thường liên quan đến điều kiện về tiếp tuyến của đường cong và đường thẳng. Học sinh cần hiểu rằng tọa độ của tiếp điểm thường là nghiệm của phương trình bậc hai mà chúng ta có thể rút gọn về phương trình bậc hai bằng định lý Viet. Kỹ thuật động não nên được sử dụng đầy đủ trong hình thức thực hành này.
>>> Có thể bạn quan tâm: CR OH 2 màu gì? Tìm hiểu thông tin về hợp chất Cr(OH)2
Dạng 6: Tương giao của 2 đồ thị và tập hợp điểm
Đây cũng là một dạng câu hỏi thường gặp trong kỳ thi tuyển sinh. Khi gặp dạng bài toán này, học sinh cần viết phương trình tọa độ giao điểm. Từ phương trình này, học sinh vận dụng định lý Viet để phát biểu biểu thức mong muốn thông qua các hệ số của phương trình. Cuối cùng, đánh giá biểu thức với các hệ số bạn vừa thay thế.
Dạng 7: Ứng dụng của 1 hệ thức truy hồi
Ứng dụng của hệ phương trình hồi quy tuyến tính giúp học sinh vận dụng và giải nhiều dạng bài tập từ cơ bản đến nâng cao. Từ đơn giản đến phức tạp.
Dạng 8: So sánh nghiệm của tam thức bậc 2 với 1 số
Các bài toán định lý nghịch đảo có dấu của tam thức bậc hai và các bài toán so sánh nghiệm của tam thức bậc hai với một số bất kỳ không còn xuất hiện trong chương trình chính khóa mà đã được giảm tải theo quy định của chương trình mới. Tuy nhiên, trong quá trình dạy học và làm bài tập, nếu học sinh biết vận dụng định lý nghịch đảo và so sánh các cách giải thì việc giải sẽ ngắn gọn hơn rất nhiều.
Định lý đảo: Cho tam thức bậc hai: f(x) = ax2 + bx +c = 0 (a khác 0). Nếu có số thực α sao cho af(α) 1;x2 và
x1 <α < x2
Kiến thức về hệ thức Viet x1-x2 đã được chúng tôi tổng hợp và mang đến những thông tin cần thiết cho các bạn. Hy vọng thông qua bài viết này các bạn sẽ củng cố và rèn luyện tư duy giải toán của mình. Sẽ có nhiều cách tiếp cận khác nhau cho mỗi vấn đề, vì vậy hãy thoải mái áp dụng những gì bạn học được một cách sáng tạo, nó sẽ giúp ích cho bạn rất nhiều sau này.
