Trong Toán học, có nhiều dạng số khác nhau được sử dụng. Để hiểu những con số này thì cần biết rằng chúng được phân loại thành các nhóm khác nhau theo đặc điểm của chúng. Cụ thể sẽ bao gồm số tự nhiên, số nguyên, số thực,… Vậy số nguyên hay giá trị nguyên là gì? Trong chia sẻ hôm nay, hãy cùng kubet77 tìm hiểu tất cả những thông tin quan trọng liên quan đến số nguyên.

Giá trị nguyên là gì?
Để hiểu rõ giá trị nguyên là gì thì cần tìm hiểu từ những khái niệm cơ bản nhất. Giá trị nguyên ở đây cũng chính là số nguyên, bao gồm số dương, số âm và cả số không nhưng không được phép có phân số.
Vì vậy, các số nguyên có thể dương {1, 2, 3, 4, 5, 6 … }, âm {−1, −2, −3, −4, -5, -6. …. } hoặc không {0}
Chúng ta có thể biểu diễn tất cả các số nguyên này cùng nhau dưới dạng: Số nguyên( Z ) = { …6, -5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6… }.. Các chấm đại diện cho vô hạn con số.
Cụ thể hơn thì đặc trưng của số nguyên sẽ là:
- Một số nguyên là bất kỳ số nào có thể là 0, hoặc số dương hoặc số âm.
- Một số nguyên không bao giờ có thể là một phân số, số thập phân hoặc phần trăm.
- Một số ví dụ về số nguyên bao gồm 2, 3, -4, 8, 99, -81, -56, v.v.
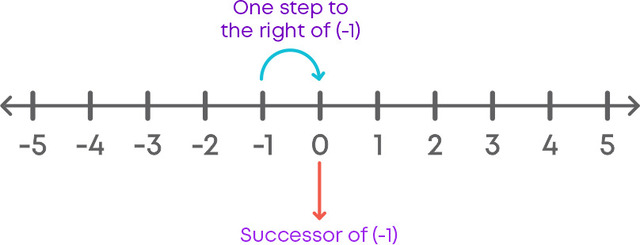
Để biểu diễn số nguyên trên trục số thì có thể nhìn vào ví dụ dưới đây. Cụ thể 0 nằm ở tâm trục số và được gọi là gốc tọa độ. Tất cả các số nguyên ở bên trái của gốc tọa độ (0) là các số nguyên âm có tiền tố là dấu trừ (-) và tất cả các số ở bên phải là các số nguyên dương có tiền tố là dấu dương (+), chúng cũng có thể được viết mà không có dấu +.
>>> Có thể bạn quan tâm: Đường cao trong tam giác cân – Tính chất & Công thức tính
Các loại số nguyên
Mặc dù khái niệm trên đây đã giải thích được giá trị nguyên là gì nhưng để hiểu rõ hơn thì nên đọc tiếp các thông tin sau. Cụ thể hãy theo dõi phân loại số nguyên bao gồm ba loại sau:
- Số dương: Số dương là những số được đặt trước bởi dấu cộng (+). Hầu hết các số dương được biểu diễn đơn giản dưới dạng các số không có dấu cộng (+). Mọi số dương đều lớn hơn 0, số âm và cả số bên trái của nó. Trên trục số, các số dương được biểu diễn bên phải gốc tọa độ (không). Ví dụ: 1, 5, 500, 66 ,89, v.v.
- Số âm: Số âm là những số có dấu trừ (-) ở phía trước. Bắt buộc phải nhắc đến dấu của số âm. Các số âm được biểu diễn ở bên trái của gốc tọa độ (không) trên một trục số. Ví dụ: -8 , -10, -1000, -1919, v.v.
- Số không: Số 0 là một số nguyên trung tính vì không thể là số nguyên dương hay số âm, tức là số 0 không có dấu +ve hoặc dấu -ve.
Các phép tính liên quan đến giá trị nguyên
Dựa vào các thuộc tính của số nguyên thì có thể áp dụng được những phép tính dưới đây:
Cộng và trừ
Các quy tắc cộng, trừ các số nguyên thực chất là các quy tắc làm việc với số dương và số âm.
Cộng hai số cùng dấu ta được kết quả cùng dấu. Khi cộng các số nguyên trái dấu thì đáp án là dấu của số có giá trị lớn hơn. Tương tự như vậy, khi cộng hai số nguyên cùng dấu thì đáp số cùng dấu. Ví dụ:
- 1 + 3 = 4
- (-4) + (-3) = -7
- 4 + 0 = 4
- 0 + (-2) = -2
Cộng các số nguyên khác dấu cũng giống như trừ các số nguyên. Câu trả lời sẽ có cùng dấu với số có giá trị lớn hơn. Ví dụ:
- (-7) + 2 = -5 cũng bằng 2 – 7
- 4 + (-8) = 4 – 8 = -4
- 3 – (-2) = 3 + 2 = 5
- (-5) – (-3) = (-5) + 3 = -2 cũng bằng 3 – 5
- 8 – 0 = 8
>>> Có thể bạn quan tâm: Vẽ tranh phong cảnh lớp 7 Đơn Giản Cực Đẹp cho học sinh
Phép nhân và phép chia
Các quy tắc nhân và chia rất đơn giản:
- Nếu cả hai số nguyên đều dương, câu trả lời là dương.
- Khi cả hai số nguyên đều âm, câu trả lời là dương. Hai dấu âm triệt tiêu lẫn nhau.
- Nếu các con số có các dấu khác nhau, câu trả lời là âm.
- Nhân bất kỳ số nguyên nào với 0 bằng 0.
- Chia cho 0 là vô cùng hoặc không xác định (tùy thuộc vào loại toán bạn đang làm).
- Nhân hoặc chia các số nguyên có cùng dấu sẽ cho bạn một số nguyên dương. Nhân hoặc chia các số trái dấu cho một số nguyên âm.
Dưới đây là các ví dụ về phép nhân và phép chia sử dụng số nguyên.
- 4 x 5 = 20
- (-2) x (-3) = 6
- (-6) x 3 = -18
- 7 x (-2) = -14
- 2 x (-3) x 4 = -24
- (-2) x 2 x (-3) = 12
- 12/2 = 6
- (-2)/6 = -1/3
- (-10)/5 = -2
- 14 / (-7) = -2
- (-6) / (-2) = 3
Hy vọng với những giải đáp và ví dụ cụ thể trên đây thì bạn có thể hiểu rõ giá trị nguyên là gì. Thêm vào đó là có thể nắm bắt được những khái niệm cơ bản liên quan đến số nguyên. Từ những kiến thức này, việc khám phá về số học và thực hiện các phép toán liên quan cũng dễ dàng hơn rất nhiều. Để biết thêm thông tin chi tiết cũng như nắm bắt thêm nhiều công thức hay liên quan đến số nguyên thì hãy truy cập vào trang chủ của chúng tôi.
