Đường cao là một kiến thức cơ bản trong toán hình học. Việc nắm chắc kiến thức về đường cao sẽ giúp bạn dễ dàng giải các bài toán. Vậy đường cao là gì và tính chất của đường cao trong tam giác cân là gì? Bài viết dưới đây kubet77.love sẽ giúp bạn có được lời giải đáp.
Tìm hiểu đường cao là gì?
Đường cao của một tam giác là đường thẳng đi qua một đỉnh của tam giác và vuông góc với cạnh đối diện của đỉnh đó. Nó cũng có thể được xác định là đường thẳng đi qua trung điểm của cạnh đối diện và đỉnh tương ứng với đường cao đó.
Mỗi tam giác đều có ba đường cao, tương ứng với từng đỉnh của tam giác. Đường cao là một khái niệm quan trọng trong hình học tam giác và được sử dụng để tính diện tích tam giác và các bài toán liên quan đến tam giác.
>>> Có thể bạn quan tâm: Vẽ tranh phong cảnh lớp 7 Đơn Giản Cực Đẹp cho học sinh
Tính chất của đường cao trong tam giác cân
Trong tam giác cân, đường cao từ đỉnh của góc nhọn cắt đôi cạnh đáy và đỉnh của tam giác và là đối tượng rất quan trọng. Dưới đây là một số tính chất của đường cao trong tam giác cân:
- Đường cao từ đỉnh của tam giác cân chia đôi cạnh đáy và vuông góc với cạnh đáy.
- Đường cao là đường trung bình của tam giác đối xứng với cạnh đáy.
- Đường cao có độ dài bằng tích của độ dài cạnh đáy và sin của góc giữa hai cạnh bên.
- Đường cao cũng là đường trung tuyến của tam giác đối xứng với cạnh đáy.
- Khoảng cách từ đỉnh của tam giác đến đường cao bằng nửa độ dài đoạn thẳng nối hai đỉnh đối của tam giác.
- Đường cao của tam giác cân cũng là đường trung trực của cạnh đáy.
- Đường cao của tam giác cân đối xứng với trục đối xứng của tam giác.
- Tam giác cân là tam giác tứ giác nội tiếp, nghĩa là đường cao từ đỉnh của tam giác cân cũng là đường cao của tứ giác nội tiếp này.
- Đường cao còn được sử dụng để tính diện tích tam giác, theo công thức: diện tích tam giác = 1/2 x đáy x đường cao.
Vì tính chất đặc biệt của nó, đường cao của tam giác cân được sử dụng rất phổ biến trong các bài toán và ứng dụng trong đời sống hàng ngày. Việc nắm chắc các kiến thức này sẽ giúp ích cho bạn rất nhiều.
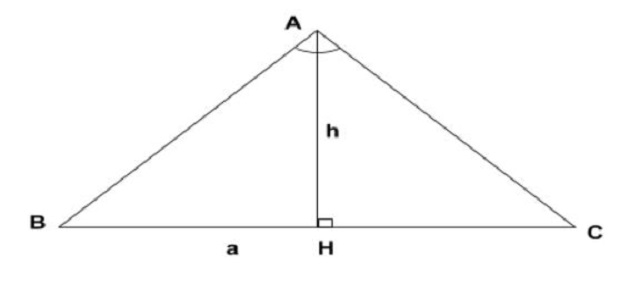
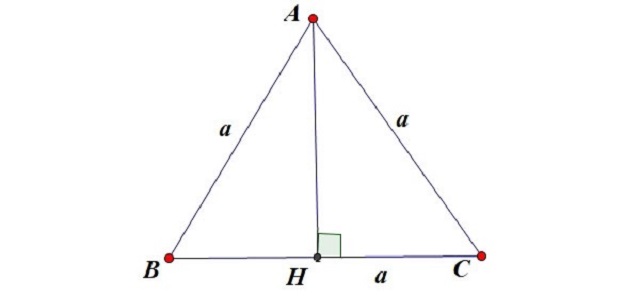
Công thức tính đường cao tam giác cân
AH^2 = AB^2 – BC^2/4
Trực tâm của tam giác là gì?
Trực tâm của tam giác là điểm trùng điểm giao của ba đường trung trực của tam giác. Ba đường trung trực này tương ứng với các cạnh của tam giác và đều vuông góc với các cạnh đó. Một cách khác, trực tâm của tam giác là trung điểm của đường thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện với đỉnh đó.
Trực tâm của tam giác có tính chất đặc biệt, đó là khi nối các trực tâm của các tam giác đồng dạng, ta được một tam giác đồng dạng với tam giác ban đầu và tỉ lệ giữa các cạnh của hai tam giác là hằng số. Ngoài ra, trực tâm của tam giác cũng là tâm đường tròn ngoại tiếp tam giác.
>>> Có thể bạn quan tâm: Top 4+ Một vài máy tính lớn khác trên thế giới mới nhất 2023
Tính chất trực tâm của tam giác
Dưới đây là một số tính chất của trực tâm trong tam giác:
- Ba đường trung trực của tam giác cắt nhau tại một điểm duy nhất, đó chính là trực tâm của tam giác.
- Trực tâm của tam giác là tâm đường tròn ngoại tiếp tam giác.
- Trực tâm nằm trên đường trung bình và đường cao của tam giác.
- Tam giác có trực tâm là tam giác đẳng giác.
- Khoảng cách giữa trực tâm và đỉnh của tam giác bằng hai phần ba độ dài đoạn thẳng nối trực tâm với đối của đỉnh đó.
- Trực tâm của tam giác là trung điểm của đường thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện với đỉnh đó.
- Trực tâm của tam giác nằm trên đường trung trực của đoạn thẳng nối trung điểm của hai cạnh của tam giác.
- Khi ta nối trực tâm của một tam giác với các đỉnh của tam giác, ta được ba đường cao của tam giác đồng dạng với tam giác ban đầu.
Ứng dụng của đường cao tam giác cân mà bạn nên biết
- Thiết kế kiến trúc: Đường cao trong tam giác cân được sử dụng để tính toán diện tích và các kích thước khác của các hình dạng tam giác cân trong thiết kế kiến trúc, ví dụ như trong việc tính toán chiều cao và kích thước của các bức tường tam giác cân.
- Đo đạc khoảng cách và độ cao: Đường cao trong tam giác cân được sử dụng để đo đạc khoảng cách và độ cao của các vật thể trong cuộc sống hàng ngày, ví dụ như đo độ cao của một cây hoặc đo khoảng cách từ một điểm đến một điểm khác.
- Trong toán học: Tam giác cân là một trong những hình học đơn giản nhất, do đó đường cao trong tam giác cân cũng được sử dụng để giải quyết các bài toán hình học, ví dụ như tính diện tích hoặc tìm độ dài các cạnh.
- Trong thực hành sản xuất: Đường cao trong tam giác cân được sử dụng trong sản xuất và gia công để tính toán vị trí của các chi tiết, đo khoảng cách hoặc độ cao giữa các chi tiết.
- Trong định lượng hóa: Đường cao trong tam giác cân được sử dụng để định lượng hóa các dữ liệu, ví dụ như đo độ cao của các vật thể trong môi trường sản xuất để tính toán sản lượng hoặc đo độ cao của các vật thể trong y tế để đưa ra các chẩn đoán.
Trên đây là toàn bộ thông tin về đường cao trong tam giác cân mà bạn không nên bỏ qua. Mong rằng với những gì đã chia sẻ sẽ giúp các bạn hiểu rõ hơn về đường cao cũng như các tính chất và ứng dụng của đường cao.
